This research proposes a method to decompose events, from large-scale video datasets, into semantic micro-events by developing a new variational inference method for the supervised LDA (sLDA), named fsLDA (Fast Supervised LDA). Class labels contain semantic information which cannot be utilized by unsupervised topic modeling algorithms such as Latent Dirichlet Allocation (LDA). In case of realistic action videos, LDA models the structure of the local features which sometimes can be irrelevant to the action. On the other hand, sLDA is intractable for large-scale datasets in regards to both time and memory. fsLDA not only overcomes the computational limitations of sLDA and achieves better results with respect to classification accuracy but also enables the variable influence of the supervised part in the inference of the topics.

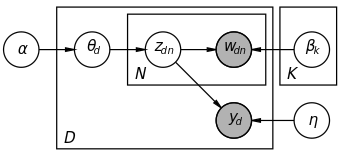
Figure 1. Probabilistic graphical model of fsLDA and sLDA

Figure 1 depicts the generative process of both sLDA and fsLDA in plate notation. This process is also outlined below (for a single document omitting document subscripts):

1. Draw topic proportions \(\theta \sim \mathrm{Dir}(\alpha)\)
2. For each codeword:
   1. Draw topic assignment \(z_n \mid \theta \sim \mathrm{Mult}(\theta)\)
   2. Draw word assignment \(w_n \mid z_n, \beta_{1:K} \sim \mathrm{Mult}(\beta_{z_n})\)
3. Draw class label \(y \mid z_{1:N} \sim \mathrm{softmax}\left( \frac{1}{N} \sum_{n=1}^N z_n, \eta \right)\) where the softmax function provides the following distribution $$p(y, \bar{z}, \eta) = \frac{\exp\left( \eta_y^T \frac{1}{N} \sum_{n=1}^N z_n \right)} {\sum_{\hat{y}=1}^C \exp\left(\eta_{\hat{y}}^T \frac{1}{N} \sum_{n=1}^N z_n\right)}$$

We use the following mean field variational family, which is also used for the unsupervised LDA, \(q(\theta, z_{1:N} \mid \gamma, \phi_{1:N}) = q(\theta \mid \gamma) \prod_{n=1}^N q(z_n \mid \phi_n)\). The Evidence Lower Bound (ELBO) is given from the following equation. The main problem that this research addresses is the intractability of the ELBO’s last term.

In [1] we derive close form update rules for the variational parameters \(\phi\) and \(\gamma\) with complexity comparable to the corresponding rules of unsupervised LDA. \(\mathcal{C}\) is a hyperparameter that controls the influence of the supervised part on the topics and \(s = \mathrm{softmax}(\mathbb{E}_q[z], \eta)\).

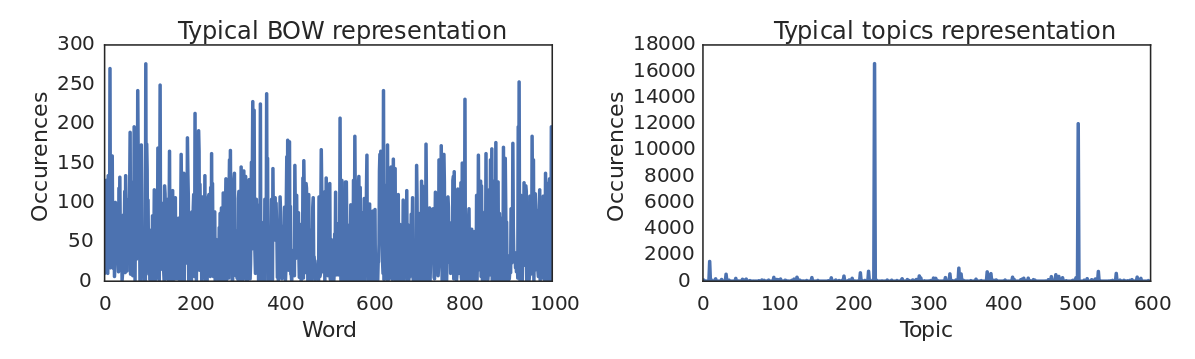
Figure 2 shows that the inferred topics can capture semantic information with respect to the action. It can be seen from the second image in Figure 2 that Improved Dense Trajectories contain a lot of irrelevant trajectories many of which do not even refer to the swinging baby. By observing the topics vs words representations, in Figure 4, it can be easily seen that the former is by far more sparse than the latter. This makes intuitive sense if we consider that all the depicted trajectories in Figure 2 clip 3 are generated by a single topic.

Figure 3. Classification accuracy using few dimensions to represent videos

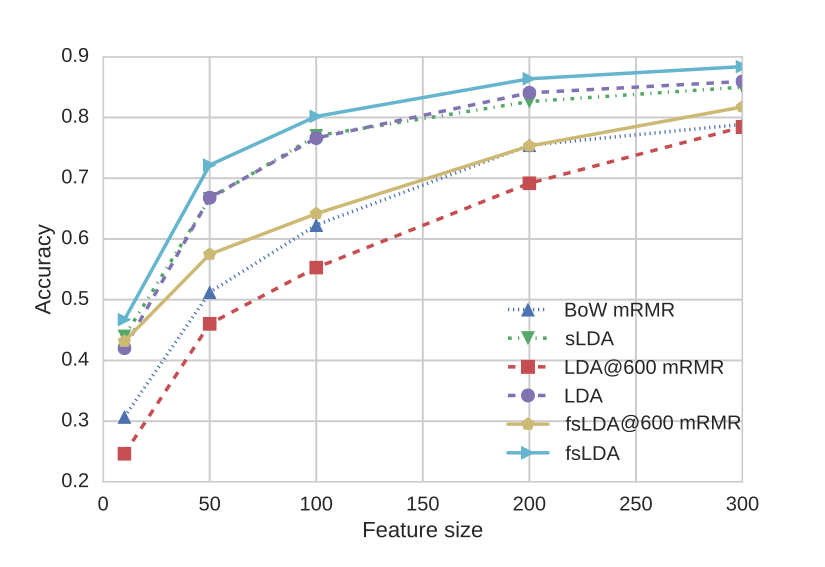
Intuitively, we expect that a topics representation is able to encode the motion or visual information of a video with less dimensions. In order to test our intuition, we reduce feature dimensionality using either minimum Redundancy Maximum Relevance Feature Selection (mRMR) or by simply training sLDA, fsLDA and LDA with various feature sizes (number of topics). Figure 3 depicts the classification performance of all the aforementioned representations. We observe that fsLDA clearly surpasses all other methods, including Bag of Visual Words.

In the following table we compare fsLDA, sLDA and LDA with respect to classification performance.

This research is accompanied by a C++ implementation of all the benchmarked algorithms (LDA, sLDA and fsLDA) under the MIT License. In order for this work to be reproducible we also publish Bag of Visual words histograms and centroids of all the local features that we have extracted from UCF11 (Youtube Action) and UCF101 (Action Recognition) datasets. The data are licensed under a Creative Commons Attribution 4.0 International license.

The entire code is organized in a C++ library, named LDA++. In addition, we also provide a set of console applications that enable the use of the implemented algorithms without writing additional code. Thorough documentation, examples and tutorials as well as the link to the Github repository can be found in the library’s homepage http://ldaplusplus.com/.

Assuming that LDA++ is already installed in your system the following terminal session trains an unsupervised LDA model with 10 topics on the MNIST Dataset after it has been converted to the appropriate numpy format. Figure 5 depicts the learned topics.

$ cd /tmp
$ wget "http://ldaplusplus.com/files/mnist.tar.gz"
$ tar -zxf mnist.tar.gz
$ lda train --topics 10 --workers 4 mnist_train.npy model.npy
E-M Iteration 1
100
...
...
$ python
Python 2.7.12 (default, Jul  1 2016, 15:12:24) 
[GCC 5.4.0 20160609] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> fig, axes = plt.subplots(1, 10, figsize=(10, 1))
>>> with open("model.npy") as f:
...     alpha = np.load(f)
...     beta = np.load(f)
...
>>> for i in xrange(10):
...     axes[i].imshow(beta[i].reshape(28, 28), cmap=plt.cm.gray_r, interpolation='nearest')
...     axes[i].set_xticks([])
...     axes[i].set_yticks([])
...
>>> plt.tight_layout()
>>> fig.savefig("mnist.png")

Data

The given data are in numpy format ready to be used with the console applications. Each file contains two numpy arrays. The first array holds the Bag of Visual Words counts and its shape is (n_words, n_videos). The second one contains the corresponding class labels of each video as integers and has shape (n_videos,). The following code snippet reads the provided data into a python session.

>>> import numpy as np
>>> with open("path/to/data") as f:
...     X = np.load(f) # transpose if you need it in sklearn compatible format
...     y = np.load(f)

Both UCF11 and UCF101 contain videos with less than 15 frames, as a result it was not feasible to extract Improved Dense Trajectories with the default configuration and those videos have been removed. Alongside each feature file we provide the corresponding filenames of the videos they were extracted from. We provide 3 random splits, in case of UCF101 we use the random splits given with the dataset. UCF11 is encoded with a vocabulary of 1000 codewords while UCF101 with 4000 codewords.